题目分析
这个题目第一眼想到的方法是暴力求解,从第i个字符开始到第j个字符,使用两层循环,依次遍历,计算是否满足偶数个元音字母,算法复杂度也很好分析$O(n^2)$,但是求解的过程中浪费了大量的运算资源,如从第一个字符到最后一个字符,对每一个字符都判断了是否为元音字符,从第二个字符到最后一个字符,对每一个字符又判断了依次,因此大大增加了时间复杂度,如果直接使用暴力法,题目是很难通过的。
暴力法
暴力法想通过这道题目也是有办法的,我们有一个先验知识,要求最长的字符串,那为何不能按照字符串长度来遍历呢?假如字符串长度为10,那么第一次遍历所有长度为10的字符串,第二次遍历所有长度为9的字符串,如果有满足条件的那一定是最优解,这样可以大大节约计算量,图解图下。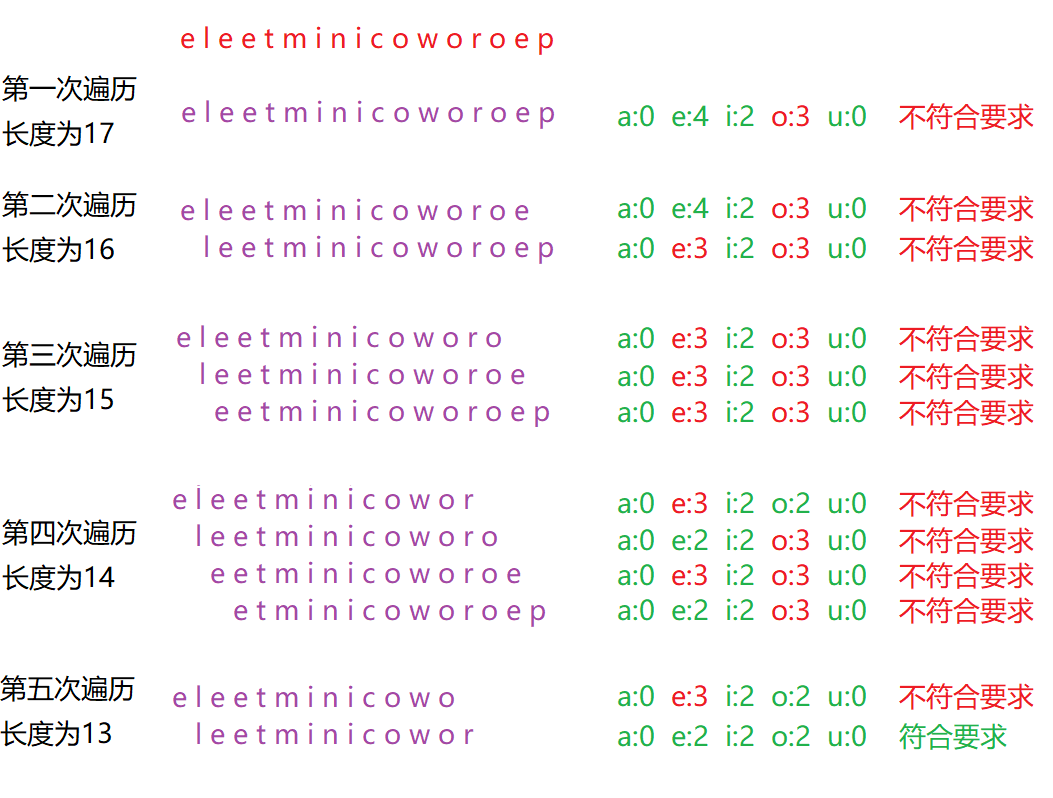
1 | class Solution: |
前缀和+状态压缩
这个思路参考官方题解,我们思考一个问题,如果中间某个字串满足条件,那么从第一个字符到该字串的前一个字符与从第一个字符到该字串的最后一个字符的状态是相同的,因此我们只需要维护一个前缀和,即可解决此问题,如下图所示。
1 | class Solution: |
题目延申
思考:如果本题改为奇数次最长的子串该如何去解?
思路还是相同的,只不过在寻找状态时要寻找完全相反的状态,如果从初始位置到某个位置的状态为(10101),那么就去寻找(01010)这个状态最早出现的位置即可。
1 | class Solution: |
刷题总结
状态压缩是一种常用的技巧,尤其在状态较多的时候,如果使用字典存储状态,则需要较大的内存,如果使用二进制位的0和1来保存状态,则只需要bit量级的内存,但是前提是每个状态的定义只有两种,比如此题的奇数和偶数,如果状态数较多,一般不使用这种方法。